Time for the next installment about coordinate systems. In my last post I talked about what a coordinate system is and gave some examples of local coordinate systems. Although local coordinate systems are quite useful, often times you’d like to specify locations on a global basis. For example, GPS tracks, locations of roads, etc.
So for today let’s see if we can come up with a way to specify locations that works for the entire Earth. To keep it as simple as possible, let’s assume that the Earth’s shape is a sphere and that the origin of our coordinate system is at the center of the Earth. Next, let’s set the z-axis to run from the Earth’s center to the north pole and make the x and y axes perpendicular to the z-axis as well as to each other.
Phew, that’s a lot of assumptions! Let’s look at this nice diagram from Richard Knippers (who maintains an informative site about coordinate reference systems that you should take a look at):
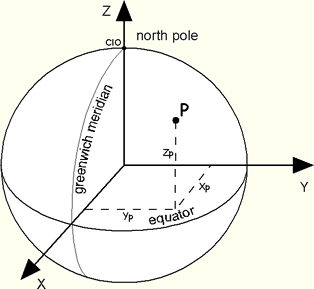
The drawing shows two other assumptions. We’ve drawn a circle around the Earth that intersects both the x-axis and y-axis and called that the equator. We have also drawn a line from the north pole to the south pole that intersects the x-axis and called that the Greenwich Meridian.
Since the origin of our coordinate system is at the center of the Earth, its is a geocentric coordinate system.
Now, how should we specify locations? One thought that jumps to mind is using simple cartesian coordinates, so each location is shown using x, y and z values. However, that turns out to be awkward to use since we’re standing on a sphere. For example, its becomes difficult to measure heights of things off the surface because two of the dimensions (x/y/z) change as you move around.
So let’s use spherical coordinates instead. We’ll say that φ measures how far above (or below) the equator we are, λ measures how far around the Earth we are from the prime meridian, and h measures the height over the surface of the Earth. Once again, here is a nice diagram from Richard Knippers:
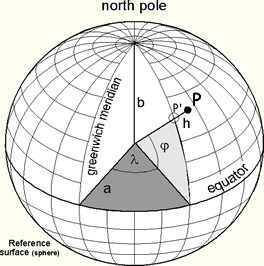
Using this system, we can now record locations as φ, λ and h values and start to share data with one another.
So we happily start marking down values until at some point we realize things aren’t lining up well. In fact, at 45 degrees north (approximately how far north Minneapolis and Portland, Oregon are in the United States) our locations are off by roughly 12 miles.
Yikes – what happened? Remember our assumption that the Earth is a perfect sphere? Well, its not. To put it non-technically, the north pole and south pole are very slightly squished in. They are each about twelve miles closer to the center of the earth than you would expect with a perfect sphere. This isn’t much, but its enough to throw off our calculations. Here is a greatly exaggerated diagram from FlightGear that shows what’s happening:
If we use a geocentric coordinate system, then we would calculate φ as the angle DBE. But if we are on the Earth’s surface, it is customary to calculate φ as the angle DBF where F is pointing straight up. In fact, the angle DBF is what we commonly called latitude. But since the Earth is slightly flat, the line FB does not intersect the Earth’s center. And this causes our measurements to be off. If you’d like a more in-depth technical discussion of this, a good place to start is Dr. T.S. Kelso’s article in the Satellite Times.
So although geocentric coordinate systems are good for rough measurements of locations on the Earth’s surface, they are not accurate enough for many uses. Instead, most maps are created using geodetic coordinate systems. We’ll cover those next, and then onto a real-world example using Google Maps.
