There is still a bit more ground work to lay before getting to the fun stuff. We’ve talked about local coordinate systems and geocentric coordinate systems. Today, let’s talk about geodetic coordinate systems.

Last time we saw that using geocentric coordinate systems results in measurement errors of approximately 12 miles on some parts of the Earth surface. The errors occur because the Earth isn’t shaped like sphere – instead, its poles are compressed in towards the center of the Earth by about 12 miles also.

So we have to come with a more sophisticated way of modeling the Earth’s surface. Not surprisingly, there is a whole science dedicated to this called geodesy. It turns out the Earth’s shape is quite irregular, and therefore difficult to model. You might think that we could do something like use mean sea level, which in technical terms is known as the geoid. But that turns out not to work very well since the geoid is also highly irregular due to local gravity anomalies caused by mountains, trenches or regional variations in the crust’s composition.

So instead we model the Earth’s surface as an ellipsoid, which for our purposes looks pretty much like a sphere but is slightly squished in along one of its axes. Here is an image from the University of Colorado’s site about coordinate systems that shows the difference between the Earth’s surface, the geoid and an ellipsoid:

Datums

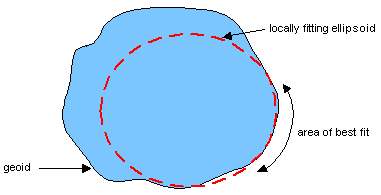
Deciding to model the Earth’s surface as an ellipsoid isn’t enough though. We have to decide the shape of the ellipsoid and how it should fit the geoid. Here is a diagram that neatly shows the issues:

The picture displays an ellipsoid that has been designed to model one part of the Earth’s surface quite accurately due both to the way it is shaped as well as the way it is fitted to the geoid. Of course, that means that it will not work very well for other parts of the Earth’s surface.

This combination of an ellipsoid and the way it is fitted to the geoid is called a geodetic datum. As you quickly see, there are an infinite number of ellipsoid combinations and fitting parameters. In fact, there are over thirty different ellipsoids in use today for mapping with names like Airy, Bessel and Clarke. And hundreds of datums!

Until recently, datums were generally designed to fit particular parts of the Earth. For example, the North American Datum of 1927, commonly abbreviated as NAD27, was designed specifically for North America (surprise, surprise) and was defined by an initial point at Meade’s Ranch in Kansas and used the Clarke 1866 ellipsoid.

However, by the 1950’s it became increasingly important to create a datum that worked world-wide. Not surprisingly, the US military led this effort (its helpful to know where things are if you want to accurately deliver ICBMs) and developed a series of world geodetic systems (abbreviated WGS). The latest of these is called WGS84, since it was released in 1984, and uses an ellipsoid whose center is at the Earth’s center. WGS84 is the system currently used by the global positioning system and therefore your GPS receiver.

Latitude and Longitude

We can now finally understand what latitude and longitude are. Latitude is the trickiest to understand. It is the angle between the equatorial plane and line that is normal (i.e., goes straight up) from the ellipsoid specified by some datum. Time for another picture from Richard Knippers:

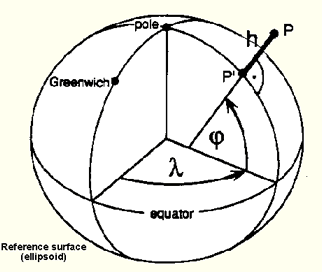
So if you’re still with me, you might realize that latitude and longitude are different depending on the datum! In fact, the difference between latitude/longitude points on the Earth’s surface can be from several hundred feet up to half a mile in extreme cases depending on the datum you are using. Thus specifying a latitude and longitude is not enough – you also have to know what datum was used to measure them.